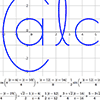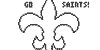math nerdiness
return to talljerome home

digital photo/illustration | math song/video | animation | other video/art | math nerdiness | new orleans


How-to video on YouTube

 
 

MORE Parametric Curve creations
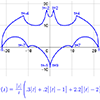
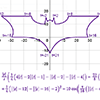
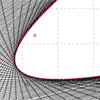
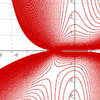
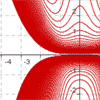
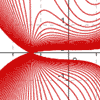
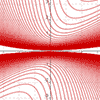
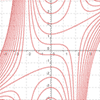
summer 2017 - Continued explorations with my process for creating complicated parametric planar curves from just a single pair of non-piecewise equations. In addition to notching up the level of diffuculty, I also made a video explaining the process.

summer 2020  - Batman Reimagined article published in NCTM journal  Mathematics Teacher: Learning & Teaching PK–12.
Single how-to video split up and reposted as this YouTube playlist of shorter videos.

Parametric Curve creations
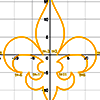
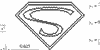
summer 2015 - Starting with an email request from a stranger, I set out to find a way to graph an entire design with just a single pair of parametric equations. The initial "jaw" logo utilized piecewise definitions, and even the second "jaw" logo used a different equation pair for each letter. Thereafter I used a variety of techniques and even included jump-discontinuity functions to incorporate multiple distinct pieces into a single equation pair.

Geogebra Lesson Materials
(Geogebra)
2012 - Click image to go to other site where I compile some of the Geogebra files that I use in my lessons for student use.

Grapher Pics
(TI-83/84 Graphing Calculators)
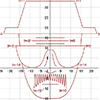
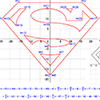
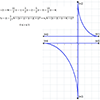
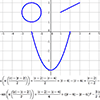
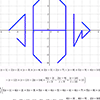
1Oct2011 - After a "batman equation" got some attention amongst nerdy circles this summer, I set out to create my own images from mathematical functions/relations.

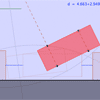
Parallel Parking
(pencil/paper and Geogebra)
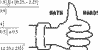
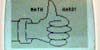
20Nov2010 update (25Dec2009 original) - After a mainstream news report on a British mathematician who derived a formula for parallel parking, I attempt to improve upon it following input and discussion with colleagues.
Updated to include metric versions of the interactive animations, plus a variation for "Perpendicular Parking."

Unit Circle Angles
(Flash)
04Oct2010 - Program to help students identify "special" angles on the x-y coordinate plane in both radian and degree measure. This is intended as a precursor to the Unit Circle Practice program I made back in May.

Unit Circle Practice
(Flash)
24May2010 - Program to help students practice evaluating basic trigonometric expressions of angles on a unit circle under time constraints.

Word Arithmetic
(pencil/paper, Excel, Flash)
21May2010 - 27 custom versions of my favorite childhood math game which I regularly solved in Dell puzzle magazines. Also see "Letter Arithmetic" programs listed below.

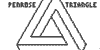
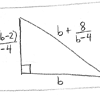
Right Triangles for which P = A
(pencil/paper)
06Jan2010 - For the past two decades my mind has continually returned to an AIME contest problem which asked: How many right triangles exist for which the perimeter in linear units is equal to the area in square units. I had found an algebraic solution long ago, but recently at a faculty meeting I started trying to find other ways to solve this problem from my youth, preferably utilizing different branches of math (algebraic, trigonometric, graphical,…). Here are the results. In short time I had five different solutions, reminding me of the beautiful interconnectedness of math by which many different paths from a single problems still lead to a shared solution.

  • Click image for PDF with full explanation and solutions

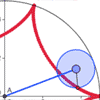
Cycloids as bounded by tangent lines
(Geogebra)
28May2009 - While cycloids are typically defined by polar equations, this exploration demonstrates them to be areas bounded by specifically-defined tangent lines.

Mathematical face
(Geogebra)
03Mar2009 - For reasons that I've since forgotten, I became compelled one day to see how well I could draw a face as a family of functions in which a single parameter is varied for a set of equations.

Sine cradle
(Geogebra)
26Feb2009 - Based on an extra credit problem I made up several years ago in which students were challenged to come up with a function whose graph is "cradled" by the basic sine wave. In this exploration, one such function graph is altered by varying a single parameter.
 

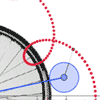
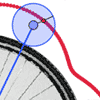
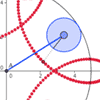
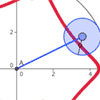
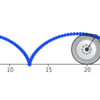
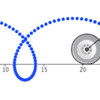
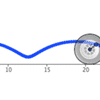
Cycloids & Trochoids as traced by a point on a rolling wheel
(Geogebra)
26Feb2009 - After a student asked me a "what if" question about a circle rolling around another circle, I launched into my own exploration into the types of shapes that can be formed by such a construction.

Buffon's Needle
(Flash)
15Feb2009 - Created after seeing a Calculus exercise concerning the mathematics behind Buffon's Needle experiment. In this experiment, the probability that a needle dropped randomly on a planar surface containing parallel lines (spaced one needle length apart) will touch a line is found to be 2/pi, or about 63.66%.

Conics as bounded by tangent lines
(Geogebra)
14Jan2009 - Based an an old-time "string art" activity, I stumbled upon some familiar shapes bounded by specifically-defined tangent lines.

Rational Functions
(Geogebra)
12Jan2009 - While using Geogebra in my Calculus class to demonstrate how horizontal, vertical, and slant asymptotes are determined by the parameters in a rational function, I inadvertently came across some interesting shapes.

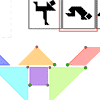
Tangrams
(Geogebra)
30Nov2008 - An exercise in which I explored some previously-unfamiliar features in Geogegra to make a computerized version of the classic tangram puzzle.

Programming teaser
(Flash)
08Oct2008 - A simple Flash animation made to familiarize students with some very basic computer code.

Cryptogame
(Flash)
10Aug2008 - Intended as a hangman-type game in which students would try to figure out words or phrases from the day's lesson, the interface turned out to be too clunky for me to use in class. A useful programming exercise for me nonetheless.

Math Dice Game
(Flash)
18Aug2007 - Computerized version of a dice game I used to play as a kid. The numbers on the white dice are to be used in a mathematical expression that equals the sum of the two black dice.

Letter Arithmetic - Division
(Flash)
25Aug2004 - Follow-up to the multiplication version of my first "Word Arithmetic" computer adaptation, involving long division instead of multiplication.

Letter Arithmetic - Multiplication
(Flash)
12Sep2003 - My ambitious first venture into Flash programming. Based on "Word Arithmetic," which were my favorites in the Dell puzzle magazines I used to buy as a kid. Each letter in the multiplication problem is randomly matched to a digit 0-9, and the player must correctly match them.